遇事不决，先考虑一个暴力 dp。

记 $dp_{i,j}$ 表示前 $i$ 位最多可以匹配 $s$ 的 $j$ 个字符的方案数，转移枚举下一位填的值 $c$，然后分类讨论：

• $j<|s|$，那么只有 $c=s_{j+1}$ 的时候会转移到 $dp_{i+1,j+1}$，否则转移到 $dp_{i+1,j}$，于是有 $dp_{i+1,j+1}\leftarrow dp_{i,j},dp_{i+1,j}\leftarrow25dp_{i,j}$；

• $j=|s|$，显然填什么都不会再转移了，所以 $dp_{i+1,j}\leftarrow26dp_{i,j}$。

直接做每次询问的复杂度是 $O(n|s|)$，显然过不了。

这是一个满足一些限制的字符串计数问题。这种 dp 本质上是在设计一个自动机，可以识别字符串，有若干个起点和若干个终点，答案就是从一个起点出发走恰好（也可能是小于或大于，具体看题目要求）$n$ 步到达一个终点的路径计数。这类问题还有一个更广为人知的名字叫做 $\mathrm{dp\ of\ dp}$，也就是 dp 套 dp。

回到这一题，本质上题目要求的就是从点 $1$ 出发，走恰好 $n$ 步到达点 $m$ 的路径计数。画出这一题的自动机，大概长成下面这样（自环上的数字表示自环的数量）：

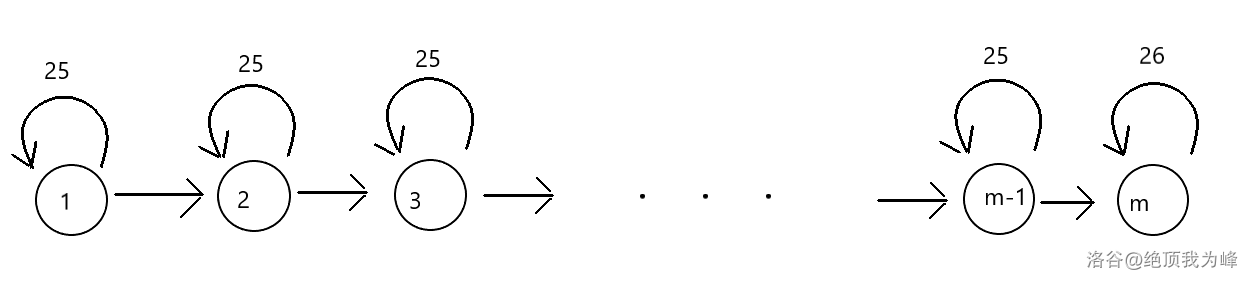
可以发现除了点 $m$ 其他点的转移是完全相同的，所以答案只与 $s$ 完成匹配的位置有关。

有了这个结论之后计算答案，直接枚举完成匹配的位置：

$f(m,n)=\sum\limits_{i=m}^n\dbinom{i-1}{m-1}25^{i-m}26^{n-i}=\sum\limits_{i=0}^{n-m}\dbinom{i+m-1}{m-1}25^i26^{n-m-i}$

很遗憾，虽然这个式子长得很像二项式定理，但是这个组合数不是很优美，只能枚举 $i$ 暴力计算。

这个做法没有前途了吗？题目限制了 $\sum |s|\leq 10^5$，也就是说本质不同的 $|s|$ 的量是 $O(\sqrt V)$ 级别的。同时注意到 $f(m,n)=26f(m,n-1)+\dbinom{n+m-1}{m-1}25^{n-m}$，因此对 $1\leq i\leq n$ 和一个给定的 $m$，$f(m,i)$ 是可以在 $O(n)$ 复杂度内全部算出来的。

于是直接对 $O(\sqrt V)$ 个不同的 $|s|$ 把 $f(|s|,i)$ 全部算出来即可，时间复杂度 $O(n\sqrt V)$。

具体实现的时候是离线的，因为离线的空间复杂度是线性的而在线不是。

#include<iostream>
#include<cstdio>
#include<vector>
#include<string>
#include<algorithm>
using namespace std;
const int lim=1e5,mod=1e9+7;
string s;
int n,len,ans[100001],cnt,fac[100001],inv[100001];
vector<pair<int,int> > v[100001];
inline int pw(int a,int b)
{
    int res=1;
    while(b)
    {
        if(b&1)
            res=1ll*res*a%mod;
        b>>=1;
        a=1ll*a*a%mod;
    }
    return res;
}
inline int c(int x,int y)
{
    return 1ll*fac[x]*inv[y]%mod*inv[x-y]%mod;
}
int main()
{
    fac[0]=inv[0]=1;
    for(int i=1;i<=lim;++i)
        fac[i]=1ll*fac[i-1]*i%mod;
    inv[lim]=pw(fac[lim],mod-2);
    for(int i=lim-1;i;--i)
        inv[i]=1ll*inv[i+1]*(i+1)%mod;
    cin>>n>>s;
    len=s.length();
    for(int i=1;i<=n;++i)
    {
        int opt;
        cin>>opt;
        if(opt==1)
        {
            cin>>s;
            len=s.length();
        }
        else
        {
            int x;
            cin>>x;
            v[len].emplace_back(x-len,++cnt);
        }
    }
    for(int i=1;i<=lim;++i)
        if(!v[i].empty())
        {
            sort(v[i].begin(),v[i].end());
            int p=0,res=0,w=1;
            for(auto j:v[i])
            {
                for(;p<=j.first;++p)
                {
                    res=(26ll*res%mod+1ll*c(p+i-1,i-1)*w%mod)%mod;
                    w=25ll*w%mod;
                }
                ans[j.second]=res;
            }
        }
    for(int i=1;i<=cnt;++i)
        cout<<ans[i]<<'\n';
    return 0;
}